Dužina

je promjer kružnice sa središtem

. Na kružnici je dana točka

takva da je
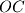
okomito na

. Na kraćem luku

odabrana je točka

. Pravci
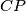
i

sijeku se u točki

, a točka

je sjecište pravca
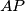
i okomice kroz

na pravac

.
Dokaži da je
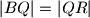
.
%V0
Dužina $\overline{AB}$ je promjer kružnice sa središtem $O$. Na kružnici je dana točka $C$ takva da je $OC$ okomito na $AB$. Na kraćem luku $BC$ odabrana je točka $P$. Pravci $CP$ i $AB$ sijeku se u točki $Q$, a točka $R$ je sjecište pravca $AP$ i okomice kroz $Q$ na pravac $AB$.
Dokaži da je $|BQ|=|QR|$.