Neka je
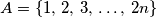
i funkcija
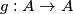
definirana sa
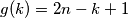
. Da li postoji funkcija
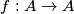
takva da je
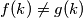
za svaki
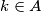
i
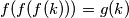
za svaki
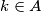
, ako je

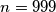
,

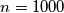
?
%V0
Neka je $A = \{1,\,2,\,3,\,\ldots,\,2n\}$ i funkcija $g : A \rightarrow A$ definirana sa $g(k)=2n-k+1$. Da li postoji funkcija $f : A \rightarrow A$ takva da je $f(k) \neq g(k)$ za svaki $k \in A$ i $f(f(f(k)))=g(k)$ za svaki $k \in A$, ako je
$a)$ $n=999$,
$b)$ $n=1000$?