Mali Fermatov teorem
Ako je tada za svaki
tada za svaki  vrijedi
vrijedi 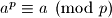 .
.
Posebno, ako je relativno prost s
relativno prost s  , gornju jednakost možemo zapisati kao
, gornju jednakost možemo zapisati kao 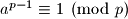 .
.
Dokaz
Koristit ćemo tvrdnju iz drugog zadatka iz ovog predavanja. (Pokušajte ga riješiti prije nego što nastavite čitati).
Kako su i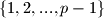 i
i 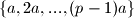 reducirani sustavi ostataka, umnožak svih njihovih elemenata mora davati isti ostatak pri dijeljenju s
reducirani sustavi ostataka, umnožak svih njihovih elemenata mora davati isti ostatak pri dijeljenju s  .
.
Dakle,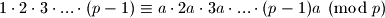 .
.
Ako pokratimo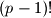 (znamo da to smijemo jer taj broj sigurno ima inverz modulo
(znamo da to smijemo jer taj broj sigurno ima inverz modulo  ) dobivamo upravo drugu tvrdnju teorema
) dobivamo upravo drugu tvrdnju teorema 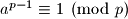 .
.
Ako je relativno prost s
relativno prost s  , smijemo cijelu jednadžbu pomnožiti s
, smijemo cijelu jednadžbu pomnožiti s  , i dobiti prvu tvrdnju teorema. Ako nije, tada je
, i dobiti prvu tvrdnju teorema. Ako nije, tada je 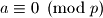 pa prva tvrdnja sigurno vrijedi.
pa prva tvrdnja sigurno vrijedi.
Ako je
 tada za svaki
tada za svaki  vrijedi
vrijedi 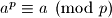 .
.Posebno, ako je
 relativno prost s
relativno prost s  , gornju jednakost možemo zapisati kao
, gornju jednakost možemo zapisati kao 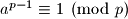 .
.Dokaz
Koristit ćemo tvrdnju iz drugog zadatka iz ovog predavanja. (Pokušajte ga riješiti prije nego što nastavite čitati).
Kako su i
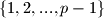 i
i 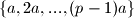 reducirani sustavi ostataka, umnožak svih njihovih elemenata mora davati isti ostatak pri dijeljenju s
reducirani sustavi ostataka, umnožak svih njihovih elemenata mora davati isti ostatak pri dijeljenju s  .
. Dakle,
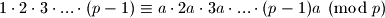 .
.Ako pokratimo
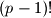 (znamo da to smijemo jer taj broj sigurno ima inverz modulo
(znamo da to smijemo jer taj broj sigurno ima inverz modulo  ) dobivamo upravo drugu tvrdnju teorema
) dobivamo upravo drugu tvrdnju teorema 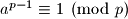 .
.Ako je
 relativno prost s
relativno prost s  , smijemo cijelu jednadžbu pomnožiti s
, smijemo cijelu jednadžbu pomnožiti s  , i dobiti prvu tvrdnju teorema. Ako nije, tada je
, i dobiti prvu tvrdnju teorema. Ako nije, tada je 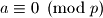 pa prva tvrdnja sigurno vrijedi.
pa prva tvrdnja sigurno vrijedi.  Školjka
Školjka