Let

be a positive integer, and consider a sequence
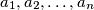
of positive integers. Extend it periodically to an infinite sequence
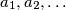
by defining
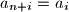
for all
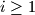
. If
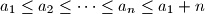
and
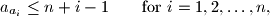
prove that
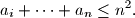
%V0
Let $n$ be a positive integer, and consider a sequence $a_1, a_2, \ldots, a_n$ of positive integers. Extend it periodically to an infinite sequence $a_1, a_2, \ldots$ by defining $a_{n+i} = a_i$ for all $i \geq 1$. If $$
a_1 \leq a_2 \leq \cdots \leq a_n \leq a_1 + n
$$ and $$
a_{a_i} \leq n + i - 1 \quad \quad \text{for}\ i = 1, 2, \ldots, n \text{,}
$$ prove that $$
a_i + \cdots + a_n \leq n^2 \text{.}
$$