Let

be a positive integer. Find the smallest integer

with the following property: Given any real numbers
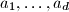
such that
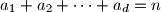
and
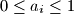
for
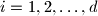
, it is possible to partition these numbers into

groups (some of which may be empty) such that the sum of the numbers in each group is at most

.
%V0
Let $n$ be a positive integer. Find the smallest integer $k$ with the following property: Given any real numbers $a_1, \ldots, a_d$ such that $a_1 + a_2 + \cdots + a_d = n$ and $0 \leq a_i \leq 1$ for $i = 1, 2, \ldots, d$, it is possible to partition these numbers into $k$ groups (some of which may be empty) such that the sum of the numbers in each group is at most $1$.