In the plane, 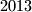 red points and
red points and 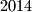 blue points are marked so that no three of the marked points are collinear. One needs to draw
blue points are marked so that no three of the marked points are collinear. One needs to draw  lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors.
lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors.
Find the minimal value of such that the goal is attainable for every possible configuration of
such that the goal is attainable for every possible configuration of 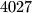 points.
points.
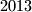 red points and
red points and 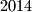 blue points are marked so that no three of the marked points are collinear. One needs to draw
blue points are marked so that no three of the marked points are collinear. One needs to draw  lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors.
lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors. Find the minimal value of
 such that the goal is attainable for every possible configuration of
such that the goal is attainable for every possible configuration of 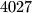 points.
points.  Školjka
Školjka