Školjka A crazy physicist discovered a new kind of particle which he called an imon, after some of them mysteriously appeared in his lab. Some pairs of imons in the lab can be entangled, and each imon can participate in many entanglement relations. The physicist has found a way to perform the following two kinds of operations with these particles, one operation at a time.
(i) If some imon is entangled with an odd number of other imons in the lab, then the physicist can destroy it.
(ii) At any moment, he may double the whole family of imons in his lab by creating a copy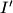
of each imon 
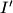. During this procedure, the two copies and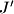 
become entangled if and only if the original imons and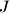 
are entangeld, and each copy 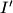becomes entangled with its original imon ; no other entanglements occur or disappear at this moment.
Prove that the physicist may apply a sequence of such operations resulting in a family of imons, no two of which are entangled.
(i) If some imon is entangled with an odd number of other imons in the lab, then the physicist can destroy it.
(ii) At any moment, he may double the whole family of imons in his lab by creating a copy
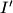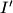of each imon . During this procedure, the two copies and 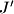become entangled if and only if the original imons and 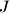are entangeld, and each copy 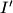becomes entangled with its original imon ; no other entanglements occur or disappear at this moment.Prove that the physicist may apply a sequence of such operations resulting in a family of imons, no two of which are entangled.