In some country several pairs of cities are connected by direct two-way flights. It is possible to go from any city to any other by a sequence of flights. The distance between two cities is defined to be the least possible number of flights required to go from one of them to the other. It is known that for any city there are at most 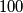 cities at distance exactly three from it. Prove that there is no city such that more than
cities at distance exactly three from it. Prove that there is no city such that more than 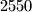 other cities have distance exactly four from it.
other cities have distance exactly four from it.
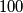 cities at distance exactly three from it. Prove that there is no city such that more than
cities at distance exactly three from it. Prove that there is no city such that more than 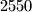 other cities have distance exactly four from it.
other cities have distance exactly four from it.  Školjka
Školjka