Let  be an integer. Consider all circular arrangements of the numbers
be an integer. Consider all circular arrangements of the numbers 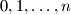 ; the
; the  rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers
rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers 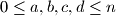 with
with 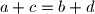 , the chord joining numbers
, the chord joining numbers  and
and  does not intersect the chord joining numbers
does not intersect the chord joining numbers  and
and  .
.
Let be the number of beautiful arrangements of
be the number of beautiful arrangements of 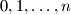 . Let
. Let  be the number of pairs
be the number of pairs 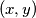 of positive integers such that
of positive integers such that 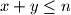 and
and 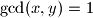 . Prove that
. Prove that 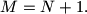
 be an integer. Consider all circular arrangements of the numbers
be an integer. Consider all circular arrangements of the numbers 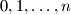 ; the
; the  rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers
rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers 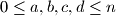 with
with 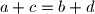 , the chord joining numbers
, the chord joining numbers  and
and  does not intersect the chord joining numbers
does not intersect the chord joining numbers  and
and  .
.Let
 be the number of beautiful arrangements of
be the number of beautiful arrangements of 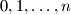 . Let
. Let  be the number of pairs
be the number of pairs 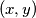 of positive integers such that
of positive integers such that 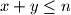 and
and 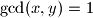 . Prove that
. Prove that 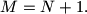
 Školjka
Školjka