In a triangle

, let

and

be the feet of the angle bisectors of angles

and

, respectively. A rhombus is inscribed into the quadrilateral
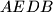
(all vertices of the rhombus lie on different sides of
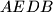
). Let
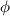
be the non-obtuse angle of the rhombus. Prove that
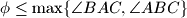
.
%V0
In a triangle $ABC$, let $D$ and $E$ be the feet of the angle bisectors of angles $A$ and $B$, respectively. A rhombus is inscribed into the quadrilateral $AEDB$ (all vertices of the rhombus lie on different sides of $AEDB$). Let $\phi$ be the non-obtuse angle of the rhombus. Prove that $\phi \leq \operatorname{max}\{ \angle BAC, \angle ABC \}$.