Prove that for any pair of positive integers

and

there exist

positive integers
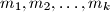
such that
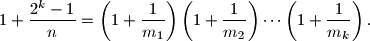
%V0
Prove that for any pair of positive integers $k$ and $n$ there exist $k$ positive integers $m_1, m_2, \ldots, m_k$ such that $$
1 + \frac{2^k - 1}{n} =
\left( 1 + \frac{1}{m_1} \right)
\left( 1 + \frac{1}{m_2} \right)
\cdots
\left( 1 + \frac{1}{m_k} \right) \text{.}
$$