Prove that there exist infinitely many positive integers
such that the largest prime divisor of
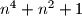
is equal to the largest prime divisor of
.
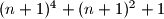
%V0
Prove that there exist infinitely many positive integers $n$ such that the largest prime divisor of $n^4 + n^2 + 1$ is equal to the largest prime divisor of $(n + 1)^4 + (n + 1)^2 + 1$.
Školjka