Determine the functions
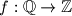
satisfying
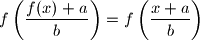
for all
,
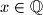
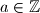
, and
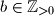
. (Here,
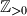
denotes the set of positive integers.)
%V0
Determine the functions $f : \mathbb{Q} \to \mathbb{Z}$ satisfying $$
f \left( \frac{f(x) + a}{b} \right ) = f \left( \frac{x + a}{b} \right )
$$ for all $x \in \mathbb{Q}$, $a \in \mathbb{Z}$, and $b \in \mathbb{Z}_{>0}$. (Here, $\mathbb{Z}_{>0}$ denotes the set of positive integers.)
Školjka