Let  be an irrational positive number, and let
be an irrational positive number, and let  be a positive integer. A pair
be a positive integer. A pair 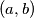 of positive integer is called good if
of positive integer is called good if 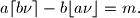
A good pair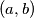 is called excellent if neither of the pairs
is called excellent if neither of the pairs 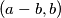 and
and 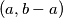 is good. (As usual, by
is good. (As usual, by 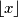 and
and 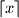 we denote the integer numbers such that
we denote the integer numbers such that 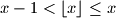 and
and 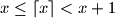 .)
.)
Prove that the number of excellent pairs is equal to the sum of the positive divisors of .
.
 be an irrational positive number, and let
be an irrational positive number, and let  be a positive integer. A pair
be a positive integer. A pair 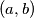 of positive integer is called good if
of positive integer is called good if 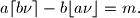
A good pair
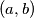 is called excellent if neither of the pairs
is called excellent if neither of the pairs 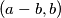 and
and 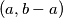 is good. (As usual, by
is good. (As usual, by 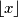 and
and 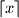 we denote the integer numbers such that
we denote the integer numbers such that 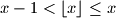 and
and 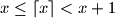 .)
.)Prove that the number of excellent pairs is equal to the sum of the positive divisors of
 .
.  Školjka
Školjka