Let  be an integer. Consider an
be an integer. Consider an 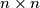 chessboard consisting of
chessboard consisting of 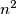 unit squares. A configuration of
unit squares. A configuration of  rooks on this board is peaceful if every row and every column contains exactly one rook. Find the greatest positive integer
rooks on this board is peaceful if every row and every column contains exactly one rook. Find the greatest positive integer  such that, for each peaceful configuration of
such that, for each peaceful configuration of  rooks, there is a
rooks, there is a 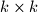 square which does not contain a rook on any of its
square which does not contain a rook on any of its 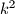 unit squares.
unit squares.
 be an integer. Consider an
be an integer. Consider an 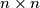 chessboard consisting of
chessboard consisting of 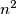 unit squares. A configuration of
unit squares. A configuration of  rooks on this board is peaceful if every row and every column contains exactly one rook. Find the greatest positive integer
rooks on this board is peaceful if every row and every column contains exactly one rook. Find the greatest positive integer  such that, for each peaceful configuration of
such that, for each peaceful configuration of  rooks, there is a
rooks, there is a 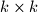 square which does not contain a rook on any of its
square which does not contain a rook on any of its 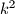 unit squares.
unit squares.  Školjka
Školjka