Neka su
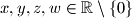
takvi da je
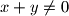
,
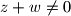
i
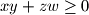
. Dokažite nejednakost
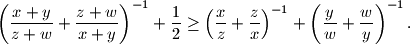
%V0
Neka su $x, y, z, w \in \mathbb{R} \setminus \{0\}$ takvi da je $x + y \neq 0$, $z + w \neq 0$ i $xy + zw \geq 0$. Dokažite nejednakost $$
\left( \frac{x + y}{z + w} + \frac{z + w}{x + y} \right)^{-1} + \frac{1}{2}
\geq
\left( \frac{x}{z} + \frac{z}{x} \right)^{-1}
+
\left( \frac{y}{w} + \frac{w}{y} \right)^{-1} \text{.}
$$