Izraz 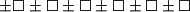 je napisan na ploči. Dva igrača,
je napisan na ploči. Dva igrača,  i
i  , igraju igru, naizmjence povlačeći poteze. Igrač
, igraju igru, naizmjence povlačeći poteze. Igrač  povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak
povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak  nekim prirodnim brojem. Nakon što su svi znakovi
nekim prirodnim brojem. Nakon što su svi znakovi  zamijenjeni, igrač
zamijenjeni, igrač  zamjenjuje svaki od predznaka
zamjenjuje svaki od predznaka 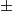 s jednim od predznaka
s jednim od predznaka  ili
ili  . Igrač
. Igrač  pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva
pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva 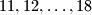 . U protivnome pobjeđuje igrač
. U protivnome pobjeđuje igrač  .
.
Koji igrač ima pobjedničku strategiju?
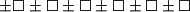 je napisan na ploči. Dva igrača,
je napisan na ploči. Dva igrača,  i
i  , igraju igru, naizmjence povlačeći poteze. Igrač
, igraju igru, naizmjence povlačeći poteze. Igrač  povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak
povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak  nekim prirodnim brojem. Nakon što su svi znakovi
nekim prirodnim brojem. Nakon što su svi znakovi  zamijenjeni, igrač
zamijenjeni, igrač  zamjenjuje svaki od predznaka
zamjenjuje svaki od predznaka 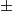 s jednim od predznaka
s jednim od predznaka  ili
ili  . Igrač
. Igrač  pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva
pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva 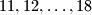 . U protivnome pobjeđuje igrač
. U protivnome pobjeđuje igrač  .
.Koji igrač ima pobjedničku strategiju?
 Školjka
Školjka