Tablica dimenzija

ispunjena je jedinicama i nulama. Poznate je da ne postoje četiri jedinice na mjestima koje čine pravokutnik. Dokažite da je broj jedinica u tablici najviše
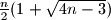
.
%V0
Tablica dimenzija $n \times n$ ispunjena je jedinicama i nulama. Poznate je da ne postoje četiri jedinice na mjestima koje čine pravokutnik. Dokažite da je broj jedinica u tablici najviše $\frac n2 (1 + \sqrt{4n - 3})$.