Na košarkaškom turniru svaka od ekipa igra točno dva puta sa svakom od ostalih ekipa. Pobjeda donosi  boda, poraz
boda, poraz  bodova, a neriješenog rezultata nema. Odredi sve prirodne brojeve
bodova, a neriješenog rezultata nema. Odredi sve prirodne brojeve  za koje postoji košarkaški turnir s
za koje postoji košarkaški turnir s  ekipa na kojem je jedna ekipa, pobjednik turnira, imala
ekipa na kojem je jedna ekipa, pobjednik turnira, imala 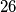 bodova, a točno dvije ekipe najmanji broj bodova, i to
bodova, a točno dvije ekipe najmanji broj bodova, i to  bodova.
bodova.
 boda, poraz
boda, poraz  bodova, a neriješenog rezultata nema. Odredi sve prirodne brojeve
bodova, a neriješenog rezultata nema. Odredi sve prirodne brojeve  za koje postoji košarkaški turnir s
za koje postoji košarkaški turnir s  ekipa na kojem je jedna ekipa, pobjednik turnira, imala
ekipa na kojem je jedna ekipa, pobjednik turnira, imala 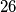 bodova, a točno dvije ekipe najmanji broj bodova, i to
bodova, a točno dvije ekipe najmanji broj bodova, i to  bodova.
bodova.  Školjka
Školjka