Za prirodni broj  kažemo da je tablica s tri retka i
kažemo da je tablica s tri retka i  stupaca
stupaca 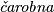 ako postoji prirodni broj
ako postoji prirodni broj 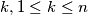 , takav da se
, takav da se
 u prvom retku nalaze redom brojevi
u prvom retku nalaze redom brojevi 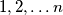 ,
,
 u drugom retku nalaze redom brojevi
u drugom retku nalaze redom brojevi 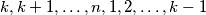 ,
,
 u trećem retku nalaze brojevi od
u trećem retku nalaze brojevi od  do
do  u takvom poretku da su zbrojevi triju brojeva u svakom stupcu međusobno jednaki.
u takvom poretku da su zbrojevi triju brojeva u svakom stupcu međusobno jednaki.
Odredi sve prirodne brojeve za koje postoje čarobna tablica i za svaki takav
za koje postoje čarobna tablica i za svaki takav  odredi koliko ima čarobnih tablica.
odredi koliko ima čarobnih tablica.
 kažemo da je tablica s tri retka i
kažemo da je tablica s tri retka i  stupaca
stupaca 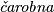 ako postoji prirodni broj
ako postoji prirodni broj 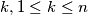 , takav da se
, takav da se u prvom retku nalaze redom brojevi
u prvom retku nalaze redom brojevi 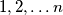 ,
, u drugom retku nalaze redom brojevi
u drugom retku nalaze redom brojevi 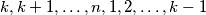 ,
, u trećem retku nalaze brojevi od
u trećem retku nalaze brojevi od  do
do  u takvom poretku da su zbrojevi triju brojeva u svakom stupcu međusobno jednaki.
u takvom poretku da su zbrojevi triju brojeva u svakom stupcu međusobno jednaki.Odredi sve prirodne brojeve
 za koje postoje čarobna tablica i za svaki takav
za koje postoje čarobna tablica i za svaki takav  odredi koliko ima čarobnih tablica.
odredi koliko ima čarobnih tablica.  Školjka
Školjka