Marko ima

kartica
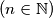
, po dvije kartice sa svakim od brojeva
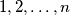
. Kada ih je promiješao i složio jednu do druge u niz, primijetio je da se za svaki

iz skupa
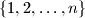
između dvije kartica s brojem

nalazi točno

drugih kartica.
Dokaži da je broj
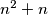
djeljiv s

.
%V0
Marko ima $2n$ kartica $(n \in \mathbb{N})$, po dvije kartice sa svakim od brojeva $1, 2, \ldots, n$. Kada ih je promiješao i složio jednu do druge u niz, primijetio je da se za svaki $k$ iz skupa $\{1, 2, \ldots, n\}$ između dvije kartica s brojem $k$ nalazi točno $k$ drugih kartica.
Dokaži da je broj $n^2 + n$ djeljiv s $4$.