Neka je  opisana kružnica trokuta
opisana kružnica trokuta  i
i  njeno središte. Kružnica
njeno središte. Kružnica  sa središtem
sa središtem  siječe dužinu
siječe dužinu  u točkama
u točkama  i
i  , tako da su točke
, tako da su točke  ,
,  ,
,  i
i  u parovima različite i leže na pravcu
u parovima različite i leže na pravcu  tim redom. Neka su
tim redom. Neka su  i
i  sjecišta kružnica
sjecišta kružnica  i
i  takva da točke
takva da točke  ,
,  ,
,  ,
,  i
i  leže na kružnici
leže na kružnici  tim redom. Neka je
tim redom. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 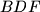 i dužine
i dužine  . Neka je
. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 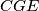 i dužine
i dužine  .
.
Pretpostavlja se da su pravci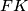 i
i 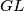 različiti i da se sijeku u točki
različiti i da se sijeku u točki  . Dokaži da točka
. Dokaži da točka  leži na pravcu
leži na pravcu 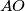 .
.
 opisana kružnica trokuta
opisana kružnica trokuta  i
i  njeno središte. Kružnica
njeno središte. Kružnica  sa središtem
sa središtem  siječe dužinu
siječe dužinu  u točkama
u točkama  i
i  , tako da su točke
, tako da su točke  ,
,  ,
,  i
i  u parovima različite i leže na pravcu
u parovima različite i leže na pravcu  tim redom. Neka su
tim redom. Neka su  i
i  sjecišta kružnica
sjecišta kružnica  i
i  takva da točke
takva da točke  ,
,  ,
,  ,
,  i
i  leže na kružnici
leže na kružnici  tim redom. Neka je
tim redom. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 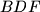 i dužine
i dužine  . Neka je
. Neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 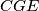 i dužine
i dužine  .
.Pretpostavlja se da su pravci
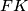 i
i 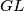 različiti i da se sijeku u točki
različiti i da se sijeku u točki  . Dokaži da točka
. Dokaži da točka  leži na pravcu
leži na pravcu 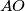 .
.  Školjka
Školjka