matsimic, 16. rujna 2015. 15:18
%V0
Postavio sam rješenje.
grga, 16. rujna 2015. 01:18
nisam nista nasao nazalost. malo me cudi sto u taj skup spadaju izmedu ostalog svi prosti brojevi oblika
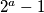
, za neki prirodni

, i prilicno sam siguran da ovaj skup nema lijepu karakterizaciju (tj "nuzan i dovoljan uvjet da netko pripada tom skupu"). jasno, ako neki skup nema "lijepu" karakterizaciju, nemora nuzno znaciti da njegov nadskup nema lijepu karakterizaciju, ali cini to "manje vjerojatnim" .. valjda,.. sta god to znacilo...
jel mozes napisati rjesenje? bas me zanima zapravo.
Postoji nužan i dovoljan uvjet za

koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti.
%V0
nisam nista nasao nazalost. malo me cudi sto u taj skup spadaju izmedu ostalog svi prosti brojevi oblika $2^a-1$, za neki prirodni $a$, i prilicno sam siguran da ovaj skup nema lijepu karakterizaciju (tj "nuzan i dovoljan uvjet da netko pripada tom skupu"). jasno, ako neki skup nema "lijepu" karakterizaciju, nemora nuzno znaciti da njegov nadskup nema lijepu karakterizaciju, ali cini to "manje vjerojatnim" .. valjda,.. sta god to znacilo...
jel mozes napisati rjesenje? bas me zanima zapravo.
[quote]Postoji nužan i dovoljan uvjet za $n$ koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti.[/quote]
matsimic, 11. rujna 2015. 18:36
Postoji nužan i dovoljan uvjet za

koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti.
%V0
Postoji nužan i dovoljan uvjet za $n$ koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti.
grga, 11. rujna 2015. 15:36
ok onda mi je jasno sto si zelio reci kao zadatak, al moram priznat da ne shvacam sto zelis dobiti kao rjesenje.
je li to zadatak kojeg si sam smislio i zamislio tako da malo razmisljamo o njemu i nisi siguran ima li tocno rjesenje,
ili postoji neko rjesenje koje se smatra konacnim i tocnim?
%V0
ok onda mi je jasno sto si zelio reci kao zadatak, al moram priznat da ne shvacam sto zelis dobiti kao rjesenje.
je li to zadatak kojeg si sam smislio i zamislio tako da malo razmisljamo o njemu i nisi siguran ima li tocno rjesenje,
ili postoji neko rjesenje koje se smatra konacnim i tocnim?
ikicic, 9. rujna 2015. 23:08
Tek sam sad skuzio da sam u objasnjenju uzeo oznaku

koja se i gore koristila. Opet sam promijenio tekst zadatka.
%V0
Tek sam sad skuzio da sam u objasnjenju uzeo oznaku $k$ koja se i gore koristila. Opet sam promijenio tekst zadatka.
Zadnja promjena:
ikicic, 9. rujna 2015. 23:08
matsimic, 9. rujna 2015. 22:23
U redu je samo naći nužan i dovoljan uvjet, makar tvrdnja koju si iznijeo nije dokazana. (https://en.wikipedia.org/wiki/Mersenne_conjectures) Definitivno je
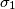
u tvrdnji zadatka, makar se vjerojatno može generalizirati na druge (može se naći opća formula za
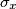
.)
%V0
U redu je samo naći nužan i dovoljan uvjet, makar tvrdnja koju si iznijeo nije dokazana. (https://en.wikipedia.org/wiki/Mersenne_conjectures) Definitivno je $ \sigma_1$ u tvrdnji zadatka, makar se vjerojatno može generalizirati na druge (može se naći opća formula za $\sigma_x$.)
Zadnja promjena:
matsimic, 9. rujna 2015. 22:23
grga, 9. rujna 2015. 22:13
moze jos malo objasnjenje?
jel zadatak: "Nađi sve

za koje postoji

takve da
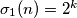
" ?
ako da, treba li mozda pisati
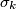
umjesto
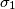
?
prilicno sam siguran da postoji cak beskonacno mnogo prostih brojeva

oblika
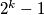
.
%V0
moze jos malo objasnjenje?
jel zadatak: "Nađi sve $n \in \mathbb{N}$ za koje postoji $k \in \mathbb{N}$ takve da $\sigma_1(n) = 2^k$ " ?
ako da, treba li mozda pisati $\sigma_k$ umjesto $\sigma_1$?
prilicno sam siguran da postoji cak beskonacno mnogo prostih brojeva $p$ oblika $2^k-1$.
ikicic, 6. rujna 2015. 21:28
Malo sam još uredio. Thx.
%V0
Malo sam još uredio. Thx.
matsimic, 6. rujna 2015. 16:05
%V0
Dodano. Sve ostalo ok?
ikicic, 6. rujna 2015. 15:50
Može objašnjenje što je
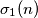
?
EDIT: Aha, naslov. Ali opet :)
%V0
Može objašnjenje što je $\sigma_1(n)$?
EDIT: Aha, naslov. Ali opet :)
Zadnja promjena:
ikicic, 6. rujna 2015. 15:50
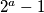 , za neki prirodni
, za neki prirodni  , i prilicno sam siguran da ovaj skup nema lijepu karakterizaciju (tj "nuzan i dovoljan uvjet da netko pripada tom skupu"). jasno, ako neki skup nema "lijepu" karakterizaciju, nemora nuzno znaciti da njegov nadskup nema lijepu karakterizaciju, ali cini to "manje vjerojatnim" .. valjda,.. sta god to znacilo...
, i prilicno sam siguran da ovaj skup nema lijepu karakterizaciju (tj "nuzan i dovoljan uvjet da netko pripada tom skupu"). jasno, ako neki skup nema "lijepu" karakterizaciju, nemora nuzno znaciti da njegov nadskup nema lijepu karakterizaciju, ali cini to "manje vjerojatnim" .. valjda,.. sta god to znacilo...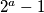 , za neki prirodni
, za neki prirodni  , i prilicno sam siguran da ovaj skup nema lijepu karakterizaciju (tj "nuzan i dovoljan uvjet da netko pripada tom skupu"). jasno, ako neki skup nema "lijepu" karakterizaciju, nemora nuzno znaciti da njegov nadskup nema lijepu karakterizaciju, ali cini to "manje vjerojatnim" .. valjda,.. sta god to znacilo...
, i prilicno sam siguran da ovaj skup nema lijepu karakterizaciju (tj "nuzan i dovoljan uvjet da netko pripada tom skupu"). jasno, ako neki skup nema "lijepu" karakterizaciju, nemora nuzno znaciti da njegov nadskup nema lijepu karakterizaciju, ali cini to "manje vjerojatnim" .. valjda,.. sta god to znacilo... koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti.
koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti. koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti.
koji sam nakon rješavanja i objave našao i online. Ako si našao uvjet, pošalji rješenje pa ćemo vidjeti. Školjka
Školjka 

 takve da je
takve da je 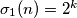 za neki
za neki  .
.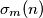 označava sumu
označava sumu  -tih potencija pozitivnih djelitelja broja
-tih potencija pozitivnih djelitelja broja  koja se i gore koristila. Opet sam promijenio tekst zadatka.
koja se i gore koristila. Opet sam promijenio tekst zadatka. 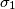 u tvrdnji zadatka, makar se vjerojatno može generalizirati na druge (može se naći opća formula za
u tvrdnji zadatka, makar se vjerojatno može generalizirati na druge (može se naći opća formula za 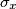 .)
.) 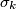 umjesto
umjesto  oblika
oblika 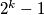 .
. 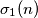 ?
?