Upisana kružnica trokuta

dira stranicu

u točki

. Neka su točke

i

, tim redom, na stranicama

i

takve da su pravci
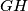
i

paralelni te da je pravac
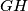
tangenta na upisanu kružnicu. Neka je točka

diralište upisane kružnice i pravca
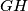
, a točka

sjecište pravaca

i
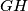
. Dokažite da vrijedi
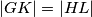
.
%V0
Upisana kružnica trokuta $ABC$ dira stranicu $\overline{BC}$ u točki $D$. Neka su točke $G$ i $H$, tim redom, na stranicama $\overline{AB}$ i $\overline{AC}$ takve da su pravci $GH$ i $BC$ paralelni te da je pravac $GH$ tangenta na upisanu kružnicu. Neka je točka $K$ diralište upisane kružnice i pravca $GH$, a točka $L$ sjecište pravaca $AD$ i $GH$. Dokažite da vrijedi $|GK|=|HL|$.