Veoma dobro poznata je nejednakost trokuta, koja govori da u svakom trokutu sa stranicama

vrijedi
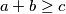
,
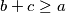
,
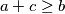
pri kojoj se jednakost postiže u degeneriranim trokutima.
Dokažite jaču nejednakost
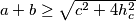
,
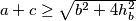
,
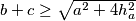
gdje su
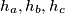
visine na stranice

. Kada se postiže jednakost?
%V0
Veoma dobro poznata je nejednakost trokuta, koja govori da u svakom trokutu sa stranicama $a, b, c$ vrijedi $a+b\geq c$, $b+c\geq a$, $a+c \geq b$ pri kojoj se jednakost postiže u degeneriranim trokutima.
Dokažite jaču nejednakost $a+b \geq \sqrt{c^2+4h_c^2}$, $a+c \geq \sqrt{b^2+4h_b^2}$, $b+c \geq \sqrt{a^2+4h_a^2}$ gdje su $h_a, h_b, h_c$ visine na stranice $a, b, c$. Kada se postiže jednakost?