Neka su
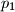
i
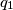
cijeli brojevi takvi da jednadžba
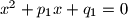
ima dva cjelobrojna rješenja. Za svaki
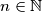
definiramo brojeve
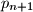
i
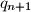
formulama
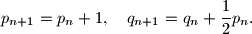
Dokaži da postoji beskonačno mnogo prirodnih brojeva

za koje jednadžba
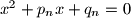
ima dva cjelobrojna rješenja.
%V0
Neka su $p_1$ i $q_1$ cijeli brojevi takvi da jednadžba $x^2 + p_1x + q_1 = 0$ ima dva cjelobrojna rješenja. Za svaki $n\in\mathbb{N}$ definiramo brojeve $p_{n+1}$ i $q_{n+1}$ formulama $$p_{n+1} = p_{n} + 1,\quad q_{n+1} = q_n + \frac{1}{2}p_n.$$
Dokaži da postoji beskonačno mnogo prirodnih brojeva $n$ za koje jednadžba $x^2 + p_nx + q_n = 0$ ima dva cjelobrojna rješenja.