Na koliko načina možemo obojati polja ploče 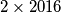 u dvije boje tako da ne postoje tri polja iste boja koja se mogu istovremeno pokriti pločicom oblika kao na slici? Pločicu je dozvoljeno rotirati.
u dvije boje tako da ne postoje tri polja iste boja koja se mogu istovremeno pokriti pločicom oblika kao na slici? Pločicu je dozvoljeno rotirati. 
Na koliko načina možemo obojati polja ploče $2 \times 2016$ u dvije boje tako da ne postoje tri polja iste boja koja se mogu istovremeno pokriti pločicom oblika kao na slici? Pločicu je dozvoljeno rotirati.
$$
\setlength{\unitlength}{10pt}
\begin{picture}(2, 2)
\put(0, 0){\line(1, 0){2}}
\put(0, 0){\line(0, 1){2}}
\put(1, 0){\line(0, 1){2}}
\put(0, 1){\line(1, 0){2}}
\put(2, 0){\line(0, 1){1}}
\put(0, 2){\line(1, 0){1}}
\end{picture}
$$