Polja ploče 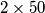 potrebno je obojati u dvije boje, crvenu i plavu, tako da budu zadovoljeni sljedeći uvjeti:
potrebno je obojati u dvije boje, crvenu i plavu, tako da budu zadovoljeni sljedeći uvjeti:
 na ploči se pojavljuju obje bolje
na ploči se pojavljuju obje bolje
 uklanjanjem svih crvenih polja ploča ostaje povezana
uklanjanjem svih crvenih polja ploča ostaje povezana
 uklanjanjem svih plavih polja ploča ostaje povezana
uklanjanjem svih plavih polja ploča ostaje povezana
Ploča je povezana ako se od svakog polja može doći do svakog drugog, prelazeći u svakom koraku s polja na njemu susjedno polje. Polja su susjedna ako imaju zajedničku stranicu.
Na koliko je načina to moguće napraviti?
Polja ploče $2 \times 50$ potrebno je obojati u dvije boje, crvenu i plavu, tako da budu zadovoljeni sljedeći uvjeti:
$\bullet$ na ploči se pojavljuju obje bolje
$\bullet$ uklanjanjem svih crvenih polja ploča ostaje povezana
$\bullet$ uklanjanjem svih plavih polja ploča ostaje povezana
Ploča je povezana ako se od svakog polja može doći do svakog drugog, prelazeći u svakom koraku s polja na njemu susjedno polje. Polja su susjedna ako imaju zajedničku stranicu.
Na koliko je načina to moguće napraviti?
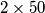 potrebno je obojati u dvije boje, crvenu i plavu, tako da budu zadovoljeni sljedeći uvjeti:
potrebno je obojati u dvije boje, crvenu i plavu, tako da budu zadovoljeni sljedeći uvjeti: na ploči se pojavljuju obje bolje
na ploči se pojavljuju obje bolje uklanjanjem svih crvenih polja ploča ostaje povezana
uklanjanjem svih crvenih polja ploča ostaje povezana uklanjanjem svih plavih polja ploča ostaje povezana
uklanjanjem svih plavih polja ploča ostaje povezana Školjka
Školjka