Let 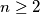 be an integer. Consider an
be an integer. Consider an 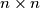 chessboard divided into
chessboard divided into 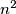 unit squares. We call a configutaion of
unit squares. We call a configutaion of  rooks on this board happy if every row and every column contains exactly one rook. Find the gretest positive integer
rooks on this board happy if every row and every column contains exactly one rook. Find the gretest positive integer  such that for every happy configuration of rooks, we can find a
such that for every happy configuration of rooks, we can find a 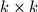 square without a rook on any of its
square without a rook on any of its 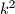 unit squares.
unit squares.
(Croatia)
 Školjka
Školjka