Let  be a set of
be a set of 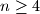 points in the plane, no three of which are collienar. Initially these points are connected with
points in the plane, no three of which are collienar. Initially these points are connected with  segments so that each point in
segments so that each point in  is the endpoint of exactly two segments. Then, at each step, one may choose two segments
is the endpoint of exactly two segments. Then, at each step, one may choose two segments  and
and  sharing a common interior point and replace them by the segments
sharing a common interior point and replace them by the segments  and
and 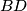 if none of them is present at this moment. Prove that it is impossible to perform
if none of them is present at this moment. Prove that it is impossible to perform 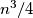 or more such moves.
or more such moves.
(Russia)
 Školjka
Školjka