Let  be a triangle with circumcircle
be a triangle with circumcircle  and incentre
and incentre  . Let the line passing through
. Let the line passing through  and perpendicular to
and perpendicular to 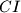 intersect the segment
intersect the segment  and the arc
and the arc  (not containing
(not containing  ) of
) of  at points
at points  and
and  , respectively. Let the line passing through
, respectively. Let the line passing through  and parallel to
and parallel to 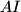 intersect
intersect 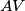 at
at  , and let the line passing through
, and let the line passing through  and parallel to
and parallel to 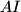 intersect
intersect  at
at  . Let
. Let  and
and  be the midpoints of
be the midpoints of 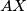 and
and  , respectively. Prove that if the points
, respectively. Prove that if the points  ,
,  , and
, and  are collinear, then the points
are collinear, then the points  ,
,  , and
, and  are also collinear.
are also collinear.
(U.S.A.)
 Školjka
Školjka