Lovac i nevidljivi zec igraju igru u euklidskoj ravnini. Početna točka zeca,  , i početna točka lovca,
, i početna točka lovca, 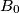 , su iste. Nakon
, su iste. Nakon  rundi igre, zec je u točki
rundi igre, zec je u točki 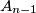 , a lovac u točki
, a lovac u točki 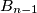 . U
. U  -toj rundi, redom se odvija sljedeće:
-toj rundi, redom se odvija sljedeće:
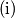 Zec se neprimjetno premješta u točku
Zec se neprimjetno premješta u točku 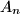 tako da je udaljenost između
tako da je udaljenost između 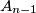 i
i 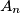 točno
točno  .
.
 Uređaj za lociranje dojavljuje lovcu točku
Uređaj za lociranje dojavljuje lovcu točku 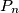 , garantirajući samo da je udaljenost itmeđu
, garantirajući samo da je udaljenost itmeđu 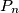 i
i 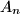 najviše
najviše  .
.
 Lovac se vidljivo premješta u točku
Lovac se vidljivo premješta u točku 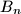 tako da je udaljenost između
tako da je udaljenost između 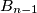 i
i 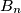 točno
točno  .
.
Može li lovac uvijek, za bilo koje pomake zeca i za bilo koje točke koje dojavi uređaj za lociranje, birati svoje poteze tako da udaljenost između njega i zeca nakon 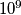 rundi bude najviše
rundi bude najviše  ?
?
Lovac i nevidljivi zec igraju igru u euklidskoj ravnini. Početna točka zeca, $A_0$, i početna točka lovca, $B_0$, su iste. Nakon $n-1$ rundi igre, zec je u točki $A_{n-1}$, a lovac u točki $B_{n-1}$. U $n$-toj rundi, redom se odvija sljedeće:
$\text{(i)}$ Zec se neprimjetno premješta u točku $A_n$ tako da je udaljenost između $A_{n-1}$ i $A_{n}$ točno $1$.
$\text{(ii)}$ Uređaj za lociranje dojavljuje lovcu točku $P_n$, garantirajući samo da je udaljenost itmeđu $P_n$ i $A_n$ najviše $1$.
$\text{(iii)}$ Lovac se vidljivo premješta u točku $B_n$ tako da je udaljenost između $B_{n-1}$ i $B_{n}$ točno $1$.
Može li lovac uvijek, za bilo koje pomake zeca i za bilo koje točke koje dojavi uređaj za lociranje, birati svoje poteze tako da udaljenost između njega i zeca nakon $10^9$ rundi bude najviše $100$?
 , i početna točka lovca,
, i početna točka lovca, 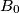 , su iste. Nakon
, su iste. Nakon  rundi igre, zec je u točki
rundi igre, zec je u točki 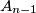 , a lovac u točki
, a lovac u točki 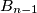 . U
. U  -toj rundi, redom se odvija sljedeće:
-toj rundi, redom se odvija sljedeće: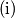 Zec se neprimjetno premješta u točku
Zec se neprimjetno premješta u točku 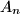 tako da je udaljenost između
tako da je udaljenost između 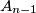 i
i 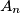 točno
točno  .
.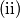 Uređaj za lociranje dojavljuje lovcu točku
Uređaj za lociranje dojavljuje lovcu točku 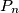 , garantirajući samo da je udaljenost itmeđu
, garantirajući samo da je udaljenost itmeđu 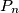 i
i 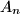 najviše
najviše  .
. Lovac se vidljivo premješta u točku
Lovac se vidljivo premješta u točku 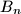 tako da je udaljenost između
tako da je udaljenost između 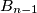 i
i 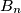 točno
točno  .
.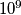 rundi bude najviše
rundi bude najviše  ?
?  Školjka
Školjka