Neka su

pozitivni realni brojevi takvi da vrijedi
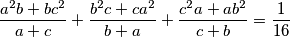
.
Dokaži da vrijedi:
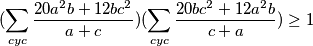
%V0
Neka su $a,b,c$ pozitivni realni brojevi takvi da vrijedi $\displaystyle{\frac{a^2b+bc^2}{a+c} + \frac{b^2c+ca^2}{b+a} + \frac{c^2a+ab^2}{c+b} = \frac{1}{16}}$.
Dokaži da vrijedi:
$$(\sum_{cyc} \frac{20a^2b+12bc^2}{a+c})(\sum_{cyc} \frac{20bc^2+12a^2b}{c+a}) \geq 1$$