Let

be a positive integer. In each of the
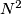
unit squares of an
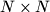
board, one of the two diagonals is drawn. The drawn diagonals divide the
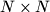
board into

regions. For each

, determine the smallest and the largest possible values of

.
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
%V0 Let $N$ be a positive integer. In each of the $N^2$ unit squares of an $N \times N$ board, one of the two diagonals is drawn. The drawn diagonals divide the $N \times N$ board into $K$ regions. For each $N$, determine the smallest and the largest possible values of $K$.
[img attachment=1 width=300px height=300px]