A positive integer 
is called a Mozartian number if the numbers 
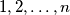together contain an even number of each digit (in base 
).
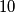Prove:
(a) All Mozartian numbers are even.
(b) There are infinitely many Mozartian numbers.
A positive integer $n$ is called a \emph{Mozartian number} if the numbers $1, 2, \ldots , n$ together contain an even number of each digit (in base $10$).
\\ \\Prove:
(a) All Mozartian numbers are even.\\
(b) There are infinitely many Mozartian numbers.
Školjka