Let  be a fixed integer with
be a fixed integer with 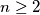 . We say that two polynomials
. We say that two polynomials  and
and  with real coefficients are block-similar if for each
with real coefficients are block-similar if for each 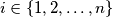 the sequences
the sequences
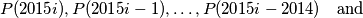
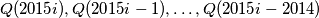
are permutations of each other.
(a) Prove that there exist distinct block-similar polynomials of degree  .
.
(b) Prove that there do not exist distinct block-similar polynomials of degree  .
.
(Canada)
 Školjka
Školjka