Let  be a triangle with
be a triangle with 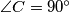 , and let
, and let 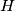 be the foot of the altitude from
be the foot of the altitude from  . A point
. A point  is chosen inside the triangle
is chosen inside the triangle 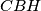 so that
so that 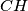 bisects
bisects 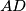 . Let
. Let  be the intersection point of the lines
be the intersection point of the lines 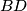 and
and 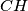 . Let
. Let 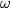 be the semicircle with diameter
be the semicircle with diameter 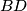 that meets the segment
that meets the segment 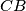 at an interior point. A line through
at an interior point. A line through  is tangent to
is tangent to 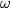 at
at  . Prove that the lines
. Prove that the lines 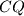 and
and 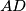 meet on
meet on 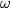 .
.
(Georgia)
 Školjka
Školjka