Let  be a convex quadrilateral, and let
be a convex quadrilateral, and let  ,
,  ,
,  , and
, and  be points on the sides
be points on the sides  ,
,  ,
,  , and
, and 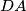 , respectively. Let the line segment
, respectively. Let the line segment 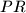 and
and 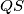 meet at
meet at  . Suppose that each of the quadrilaterals
. Suppose that each of the quadrilaterals 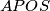 ,
, 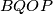 ,
, 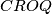 , and
, and 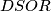 has an incircle. Prove that the lines
has an incircle. Prove that the lines  ,
,  , and
, and 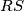 are either concurrent or parallel to each other.
are either concurrent or parallel to each other.
Let $ABCD$ be a convex quadrilateral, and let $P$, $Q$, $R$, and $S$ be points on the sides $AB$, $BC$, $CD$, and $DA$, respectively. Let the line segment $PR$ and $QS$ meet at $O$. Suppose that each of the quadrilaterals $APOS$, $BQOP$, $CROQ$, and $DSOR$ has an incircle. Prove that the lines $AC$, $PQ$, and $RS$ are either concurrent or parallel to each other.
\begin{flushright}\emph{(Bulgaria)}\end{flushright}