An integer 
is called Silesian if there exist positive integers 
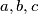such that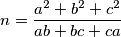 
a) Prove that there are infinitely many Silesian integers.
b) Prove that not all positive integers are Silesian.
An integer $n$ is called \emph{Silesian} if there exist positive integers $a, b, c$ such that
$$n = \frac{a^2+b^2+c^2}{ab+bc+ca}$$
a) Prove that there are infinitely many Silesian integers.
b) Prove that not all positive integers are Silesian.
Školjka