There is a lamp on each cell of a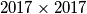 
board. Each lamp is either on or off. A lamp is called bad if it has an even number of neighbours that are on. What is the smallest possible number of bad lamps on such a board?
(Two lamps are neighbours if their respective cells share a side.)
There is a lamp on each cell of a $2017 \times 2017$ board. Each lamp is either on or off. A lamp is called \emph{bad} if it has an even number of neighbours that are on. What is the smallest possible number of bad lamps on such a board?\\
(Two lamps are neighbours if their respective cells share a side.)
Školjka