Let 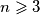 be an integer. A sequence
be an integer. A sequence 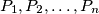 of distinct points in the plane is called good if no three of them are collinear, the polyline
of distinct points in the plane is called good if no three of them are collinear, the polyline 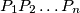 is non-self-intersecting and the triangle
is non-self-intersecting and the triangle 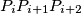 is oriented counterclockwise for every
is oriented counterclockwise for every 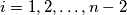 . For every integer
. For every integer 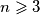 determine the greatest possible integer
determine the greatest possible integer  with the following property: there exist
with the following property: there exist  distinct points
distinct points 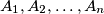 in the plane for which there are
in the plane for which there are  distinct permutations
distinct permutations 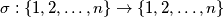 such that
such that 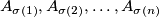 is good.
is good.
(A polyline 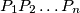 consists of the segments
consists of the segments 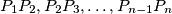 .)
.)
 Školjka
Školjka