Let  be an acute-angled triangle with
be an acute-angled triangle with  and circumcircle
and circumcircle  . Let
. Let  be the midpoint of the shorter arc
be the midpoint of the shorter arc  of
of  , and let
, and let  be the intersection of the rays
be the intersection of the rays  and
and 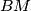 . Let
. Let 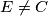 be the intersection of the internal bisector of the angle
be the intersection of the internal bisector of the angle 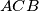 and the circumcircle of the triangle
and the circumcircle of the triangle 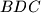 . Let us assume that
. Let us assume that  is inside the triangle
is inside the triangle  and there is an intersection
and there is an intersection  of the line
of the line 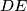 and the circle
and the circle  such that
such that  is the midpoint of the segment
is the midpoint of the segment 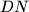 .
.
Show that  is the midpoint of the segment
is the midpoint of the segment 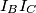 , where
, where 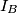 and
and 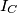 are the excentres of
are the excentres of  opposite to
opposite to  and
and  , respectively.
, respectively.
 Školjka
Školjka