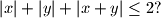Slični zadaci
Za kupnju školskog autobusa koji će prevoziti djecu iz četiri mjesta  ,
,  ,
,  ,
,  potrebno je
potrebno je 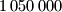 kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu
kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu  je stanovnika koliko u mjestima
je stanovnika koliko u mjestima  i
i  zajedno, u mjestu
zajedno, u mjestu  je
je 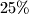 manje stanovnika nego u
manje stanovnika nego u  , a
, a 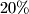 više nego u
više nego u  . Odredi kolike će iznose platiti pojedina mjesta.
. Odredi kolike će iznose platiti pojedina mjesta.
 ,
,  ,
,  ,
,  potrebno je
potrebno je 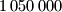 kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu
kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu  je stanovnika koliko u mjestima
je stanovnika koliko u mjestima  i
i  zajedno, u mjestu
zajedno, u mjestu  je
je 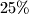 manje stanovnika nego u
manje stanovnika nego u  , a
, a 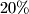 više nego u
više nego u  . Odredi kolike će iznose platiti pojedina mjesta.
. Odredi kolike će iznose platiti pojedina mjesta.  Školjka
Školjka 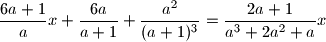 u ovisnosti o realnom parametru
u ovisnosti o realnom parametru  .
.  ,
,  ,
,  ako je
ako je 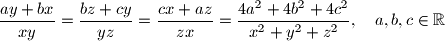
 takav da postoji niz od
takav da postoji niz od 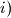 zbroj svaka tri uzastopna člana niza je pozitivan,
zbroj svaka tri uzastopna člana niza je pozitivan,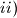 zbroj svakih pet uzastopnih članova niza je negativan.
zbroj svakih pet uzastopnih članova niza je negativan. 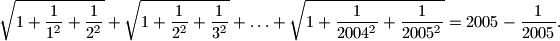
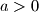 , odredite najmanju vrijednost funkcije
, odredite najmanju vrijednost funkcije 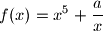 za
za 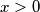 .
.