Anti-Pascalov trokut je tablica u obliku jednakostraničnog trokuta koja se sastoji od brojeva tako da, osim za brojeve u posljednjem retku, vrijedi da je svaki broj jednak apsolutnoj vrijednosti razlike dva broja koji su neposredno ispod njega. Na primjer, sljedeća tablica je anti-Pascalov trokut sa četiri retka, koji se sastoji od svih prirodnih brojeva od  do
do  .
. 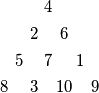 Da li postoji anti-Pascalov trokut sa
Da li postoji anti-Pascalov trokut sa 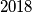 redaka, koji se sastoji od svih prirodnih brojeva od
redaka, koji se sastoji od svih prirodnih brojeva od  do
do 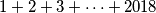 ?
?
 Školjka
Školjka