Prijateljice Anica i Neda igraju igru tako da u svakom potezu, nakon što jedna od njih kaže broj  , druga mora reći neki broj oblika
, druga mora reći neki broj oblika  pri čemu su
pri čemu su  i
i  prirodni brojevi za koje vrijedi
prirodni brojevi za koje vrijedi 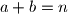 . Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj
. Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj 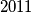 ?
?
 , druga mora reći neki broj oblika
, druga mora reći neki broj oblika  pri čemu su
pri čemu su  i
i  prirodni brojevi za koje vrijedi
prirodni brojevi za koje vrijedi 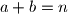 . Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj
. Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj 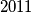 ?
?  Školjka
Školjka