Dan je paralelogram
sa šiljastim kutom u vrhu
. Na pravcu
odabrana je točka
, različita od
, tako da je
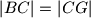
, a na pravcu
točka
, različita od
, tako da je
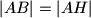
. Dokaži da je trokut
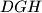
jednakokračan.
%V0
Dan je paralelogram $ABCD$ sa šiljastim kutom u vrhu $A$. Na pravcu $AB$ odabrana je točka $G$, različita od $B$, tako da je $|BC|=|CG|$, a na pravcu $BC$ točka $H$, različita od $B$, tako da je $|AB|=|AH|$. Dokaži da je trokut $DGH$ jednakokračan.
Školjka