Školjka

Sir Alex plays the following game on a row of 9 cells. Initially, all cells are empty. In each move, Sir Alex is allowed to perform exactly one of the following two operations: (1) Choose any number of the form 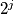$2^j$, where 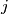$j$ is a non-negative integer, and put it into an empty cell. (2) Choose two (not necessarily adjacent) cells with the same number in them; denote that number by 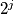$2^j$. Replace the number in one of the cells with 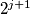$2^{j+1}$ and erase the number in the other cell. At the end of the game, one cell contains 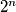$2^n$, where $n$ is a given positive integer, while the other cells are empty. Determine the maximum number of moves that Sir Alex could have made, in terms of $n$.