Školjka

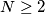Let $N \geq 2$ be an integer. 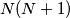$N(N+1)$ soccer players, no two of the same height, stand in a row in some order. Coah Ralph wants to remove 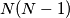$N(N -1)$ people from this row so that in the remaining row of 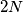$2N$ players, no one stands between the two tallest ones, no one stands between the third and the fourth tallest ones, ... , and finally no one stands between the two shortest ones. Show that this is always possible