Let  be a given positive integer. In the Cartesian plane, each lattice point with nonnegative coordinates initially contains a butterfly, and there are no other butterflies. The neighborhood of a lattice point
be a given positive integer. In the Cartesian plane, each lattice point with nonnegative coordinates initially contains a butterfly, and there are no other butterflies. The neighborhood of a lattice point  consists of all lattice points within the axis-aligned
consists of all lattice points within the axis-aligned 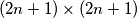 square entered at
square entered at  , apart from
, apart from  itself. We call a butterfly lonely, crowded, or comfortable, depending on whether the number of butterflies in its neighborhood
itself. We call a butterfly lonely, crowded, or comfortable, depending on whether the number of butterflies in its neighborhood  is respectively less than, greater than, or equal to half of the number of lattice points in
is respectively less than, greater than, or equal to half of the number of lattice points in  . Every minute, all lonely butterflies fly away simultaneously. This process goes on for as long as there are any lonely butterflies. Assuming that the process eventually stops, determine the number of comfortable butterflies at the final state.
. Every minute, all lonely butterflies fly away simultaneously. This process goes on for as long as there are any lonely butterflies. Assuming that the process eventually stops, determine the number of comfortable butterflies at the final state.
Let $n$ be a given positive integer. In the Cartesian plane, each lattice point with nonnegative coordinates initially contains a butterfly, and there are no other butterflies. The neighborhood of a lattice point $c$ consists of all lattice points within the axis-aligned $(2n+1) \times (2n+1)$ square entered at $c$, apart from $c$ itself. We call a butterfly lonely, crowded, or comfortable, depending on whether the number of butterflies in its neighborhood $N$ is respectively less than, greater than, or equal to half of the number of lattice points in $N$. Every minute, all lonely butterflies fly away simultaneously. This process goes on for as long as there are any lonely butterflies. Assuming that the process eventually stops, determine the number of comfortable butterflies at the final state.
 be a given positive integer. In the Cartesian plane, each lattice point with nonnegative coordinates initially contains a butterfly, and there are no other butterflies. The neighborhood of a lattice point
be a given positive integer. In the Cartesian plane, each lattice point with nonnegative coordinates initially contains a butterfly, and there are no other butterflies. The neighborhood of a lattice point  consists of all lattice points within the axis-aligned
consists of all lattice points within the axis-aligned 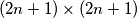 square entered at
square entered at  , apart from
, apart from  itself. We call a butterfly lonely, crowded, or comfortable, depending on whether the number of butterflies in its neighborhood
itself. We call a butterfly lonely, crowded, or comfortable, depending on whether the number of butterflies in its neighborhood  is respectively less than, greater than, or equal to half of the number of lattice points in
is respectively less than, greater than, or equal to half of the number of lattice points in  . Every minute, all lonely butterflies fly away simultaneously. This process goes on for as long as there are any lonely butterflies. Assuming that the process eventually stops, determine the number of comfortable butterflies at the final state.
. Every minute, all lonely butterflies fly away simultaneously. This process goes on for as long as there are any lonely butterflies. Assuming that the process eventually stops, determine the number of comfortable butterflies at the final state.  Školjka
Školjka