Let  and
and  be distinct positive integers. The following infinite process takes place on an initially empty board.
be distinct positive integers. The following infinite process takes place on an initially empty board.
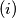 If there is at least a pair of equal numbers on the board, we choose such a pair and increase one of its components by
If there is at least a pair of equal numbers on the board, we choose such a pair and increase one of its components by  and the other by
and the other by  .
.
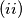 If no such pair exists, we write two times the number
If no such pair exists, we write two times the number 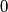 .
.
Prove that, no matter how we make the choices in 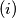 , operation
, operation 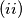 will be performed only finitely many times.
will be performed only finitely many times.
 Školjka
Školjka